Principales Aplicaciones de la Investigación de Operaciones: El Poder de la Optimización

En un mundo empresarial y social cada vez más interconectado y sujeto a limitaciones (recursos, tiempo, costos), la toma de decisiones efectivas se ha vuelto un desafío monumental. ¿Cómo asignar recursos escasos de manera óptima? ¿Cómo diseñar sistemas de servicio eficientes? ¿Cómo planificar la producción o la logística minimizando costos? La respuesta a estas y muchas otras preguntas críticas se encuentra, en gran medida, en la Investigación de Operaciones (IO).

Esta disciplina científica, armada con matemáticas, estadística y modelado computacional, proporciona un conjunto de herramientas poderosas para analizar sistemas complejos, evaluar alternativas y recomendar el mejor curso de acción basado en objetivos claramente definidos.

En este artículo exploraremos las principales aplicaciones de la IO, pilares fundamentales que transforman datos en decisiones inteligentes.

¿Qué es la Investigación de Operaciones?

La Investigación de Operaciones es una disciplina que aplica métodos analíticos avanzados para ayudar a tomar mejores decisiones. Su esencia radica en:

1. Comprender el Sistema: Identificar y definir claramente el problema, sus objetivos (maximizar beneficios, minimizar costos, optimizar servicio) y las restricciones (recursos limitados, tiempo, capacidades).
2. Construir un Modelo: Crear una representación simplificada, pero matemáticamente rigurosa, de la realidad del problema. Este modelo puede ser matemático (ecuaciones, inecuaciones), de simulación o heurístico.
3. Obtener Soluciones: Utilizar técnicas matemáticas, estadísticas y algoritmos computacionales para derivar soluciones cuantitativas a partir del modelo. Esto implica encontrar valores óptimos o casi óptimos para las variables de decisión.
4. Validar e Implementar: Probar la solución del modelo contra la realidad, ajustar si es necesario y, finalmente, implementar la solución recomendada.
5. Monitorear y Ajustar: Evaluar el desempeño de la solución implementada y realizar ajustes a medida que cambian las condiciones.

En esencia, la IO actúa como un “GPS” para la toma de decisiones complejas, guiando hacia la ruta más eficiente y efectiva posible.

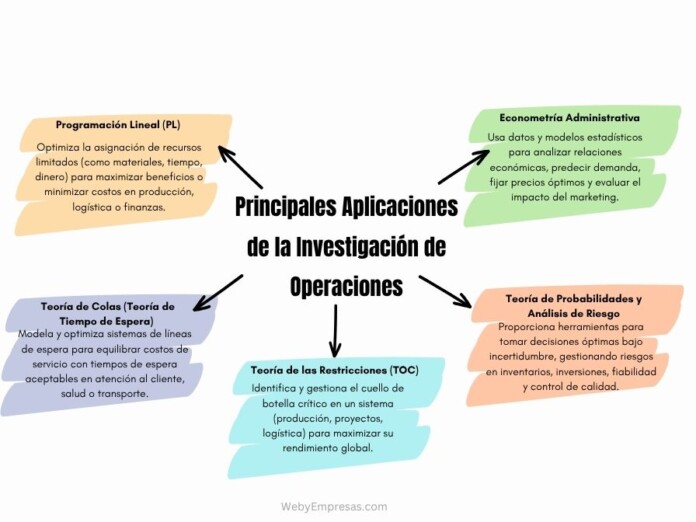
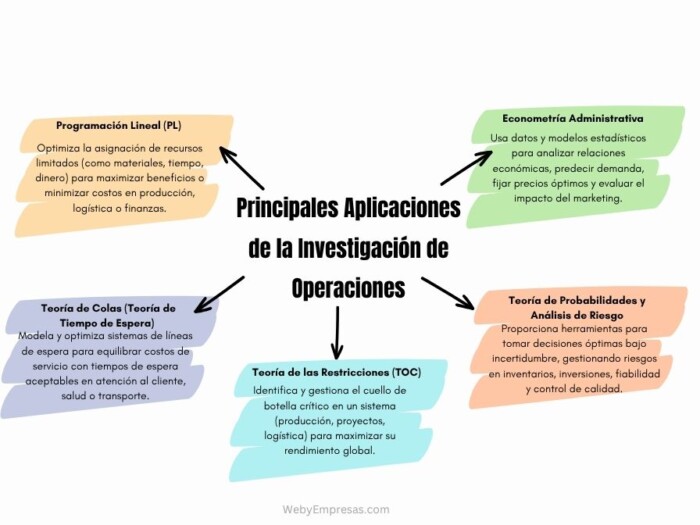
Principales Aplicaciones de la Investigación de Operaciones

Las herramientas de la IO son vastas, pero algunas destacan por su amplitud de aplicación e impacto. Veamos las principales:

1. Programación Lineal (PL) – Optimización de Recursos Escasos

Es la técnica de IO más conocida y utilizada. Se emplea para optimizar (maximizar o minimizar) una función objetivo lineal (como beneficios o costos) sujeta a un conjunto de restricciones también lineales (como disponibilidad de materias primas, horas de mano de obra, capacidad de producción).

• Aplicaciones:

• Planificación de Producción:Determinar la mezcla óptima de productos a fabricar para maximizar beneficios o minimizar costos, respetando capacidades de máquinas, disponibilidad de materiales y demanda del mercado.
• Mezcla de Ingredientes (Blending):En industrias como petroquímica, alimentaria o farmacéutica, encontrar la combinación óptima de materias primas para producir un producto final con especificaciones requeridas al menor costo posible (ej: mezcla de gasolinas, alimentos balanceados).
• Planificación Financiera:Asignar un presupuesto de inversión limitado entre diferentes proyectos para maximizar el retorno total o minimizar el riesgo.
• Asignación de Personal:Determinar cuántos empleados se necesitan en diferentes turnos o departamentos para cubrir la demanda de servicio al menor costo laboral.
• Logística y Transporte (Problema de Transporte/Asignación):Determinar las rutas más cortas o los patrones de envío desde múltiples orígenes (fábricas, almacenes) a múltiples destinos (clientes, tiendas) minimizando los costos totales de transporte. Asignar tareas a trabajadores o máquinas minimizando el tiempo o el costo total.
• Planificación Agrícola:Optimizar el uso de la tierra, cultivos, fertilizantes y agua para maximizar la producción o los ingresos.

2. Teoría de Colas (Teoría de Tiempo de Espera) – Gestionando la Congestión

Estudia matemáticamente los fenómenos de colas o líneas de espera. Analiza cómo los “clientes” (personas, piezas, llamadas telefónicas, aviones) llegan a un “servicio” (cajero, máquina, operador, pista), esperan en una cola, son atendidos y se marchan. Su objetivo es comprender y optimizar el desempeño del sistema, equilibrando costos de servicio (más servidores) con costos de espera (clientes insatisfechos, inactividad).

• Aplicaciones:

• Diseño de Centros de Llamadas:Determinar el número óptimo de agentes telefónicos necesarios para manejar la demanda de llamadas con un tiempo de espera aceptable.
• Diseño de Sistemas de Salud:Optimizar la cantidad de consultorios, equipos médicos (como resonadores) o personal de triaje en hospitales y clínicas para reducir tiempos de espera de pacientes.
• Operaciones de Retail y Bancos:Dimensionar el número de cajeros o puntos de servicio para minimizar las colas de clientes, especialmente en horas pico.
• Sistemas de Transporte:Diseñar peajes, controles de seguridad en aeropuertos o intersecciones semaforizadas para mejorar el flujo y reducir congestiones.
• Diseño de Redes de Computadoras:Analizar el tráfico de datos en routers y servidores para dimensionar capacidad y evitar cuellos de botella que ralenticen la red.
• Logística de Almacenes:Optimizar el número de muelles de carga/descarga o equipos de manipulación para minimizar el tiempo de espera de los camiones.

3. Teoría de las Restricciones (TOC) – Enfocándose en el Cuello de Botella

Desarrollada por Eliyahu Goldratt, la TOC se centra en identificar y gestionar la restricción más limitante (el “cuello de botella”) dentro de un sistema. Parte de la premisa de que el desempeño global de cualquier sistema está determinado por su restricción más crítica. Su metodología se enfoca en explotar al máximo la capacidad de la restricción, subordinar todo lo demás a esa decisión y elevar la capacidad de la restricción.

• Aplicaciones:

• Manufactura:Identificar la máquina o proceso más lento en una línea de producción (el cuello de botella) y reorganizar toda la producción para maximizar su utilización, evitando que acumule trabajo innecesario antes de ella. Esto aumenta drásticamente el throughput (tasa de generación de dinero a través de las ventas).
• Gestión de Proyectos (Cadena Crítica):Identificar la secuencia de tareas que determina la duración mínima del proyecto (la “cadena crítica”) y gestionar los recursos y los buffers (colchones de tiempo) para protegerla de las incertidumbres, reduciendo los plazos totales.
• Logística y Distribución:Identificar restricciones en la red de suministro (almacén central con capacidad limitada, ruta de transporte saturada) y optimizar los flujos para maximizar la entrega a clientes.
• Ventas y Marketing:Identificar la restricción en el proceso de ventas (por ejemplo, capacidad de los vendedores senior para cerrar tratos complejos) y alinear esfuerzos para maximizar su impacto.
• Servicios:Aplicar los principios para identificar y eliminar cuellos de botella en procesos administrativos, atención al cliente o entrega de servicios.

4. Teoría de Probabilidades y Análisis de Riesgo – Decidiendo bajo Incertidumbre

Muchas decisiones se toman en entornos donde los resultados futuros no son predecibles con certeza. La teoría de probabilidades proporciona el marco matemático para cuantificar la incertidumbre. La IO la utiliza para modelar sistemas estocásticos (donde el azar juega un papel) y analizar riesgos asociados a diferentes decisiones.

• Aplicaciones:

• Gestión de Inventarios:Modelar la demanda incierta de productos para determinar niveles óptimos de inventario (punto de reorden, cantidad a pedir) que minimicen costos totales (almacenamiento, falta de stock).
• Planificación Financiera y Análisis de Inversiones:Evaluar proyectos de inversión considerando la variabilidad en flujos de caja, tasas de interés o costos, utilizando técnicas como el árbol de decisiones, simulación Monte Carlo o Valor en Riesgo (VaR).
• Fiabilidad y Mantenimiento:Predecir la probabilidad de falla de equipos o sistemas para planificar estrategias de mantenimiento preventivo o predictivo óptimas.
• Modelos de Colas Avanzados:Como vimos, la Teoría de Colas se basa fuertemente en distribuciones de probabilidad para modelar tiempos de llegada y servicio.
• Control de Calidad Estadístico:Utilizar técnicas estadísticas basadas en muestreo y probabilidad para monitorear y controlar procesos de producción.
• Seguros:Calcular primas y reservas basándose en modelos actuariales que predicen la frecuencia y severidad de siniestros futuros.

5. Econometría Administrativa – Uniendo Datos, Economía y Decisiones

Si bien la econometría es un campo por derecho propio, su aplicación en el contexto de la toma de decisiones empresariales es una poderosa herramienta dentro del arsenal de la IO. Combina teoría económica, matemáticas, estadística y datos para estimar relaciones cuantitativas entre variables económicas y empresariales. Permite medir el impacto de decisiones pasadas y prever el efecto de futuras acciones.

• Aplicaciones:

• Previsión de Ventas y Demanda:Desarrollar modelos estadísticos que predigan la demanda futura de productos o servicios basándose en variables como precios, publicidad, ingresos del consumidor, estacionalidad y variables macroeconómicas.
• Análisis de Precios:Estimar la elasticidad-precio de la demanda para determinar el precio óptimo que maximice ingresos o beneficios. Evaluar el impacto de promociones y descuentos.
• Evaluación de Marketing:Medir la efectividad de campañas publicitarias y canales de marketing mediante modelos que aíslan su impacto en las ventas.
• Análisis de Costos:Desarrollar funciones de costos que relacionen los costos totales con los niveles de producción y otros factores, permitiendo un mejor control y planificación.
• Estudios de Mercado:Analizar datos de encuestas y comportamiento del consumidor para entender preferencias, segmentar mercados y evaluar la aceptación de nuevos productos.
• Modelos Macroeconómicos para la Empresa:Evaluar cómo cambios en el PIB, tasas de interés, inflación o tipo de cambio afectan a la demanda de la empresa, costos de insumos importados o estrategias de inversión.

Conclusión:

La Investigación de Operaciones no es solo un conjunto de técnicas aisladas; es una filosofía de pensamiento analítico y basado en datos para la mejora continua. Las aplicaciones descritas, Programación Lineal, Teoría de Colas, Teoría de las Restricciones, Teoría de Probabilidades y Econometría Administrativa, representan pilares fundamentales que abarcan desde la optimización determinista de recursos hasta la toma de decisiones bajo incertidumbre y el análisis predictivo de relaciones económicas.