El conocimiento circula de lo general a lo particular, en tal sentido la explicación de fenómenos nuevos puede estudiarse por la relación que guarda con eventos de un mismo fenómeno que es lo que frecuentemente se hace en el ámbito de las investigaciones. Debido a lo anterior expuesto mana la necesidad de establecer la relación entre dos variables cuantitativas en un grupo de sujetos de estudio.
La ciencia de las estadísticas dispone de métodos que permiten medir dicha relación, con los siguientes objetivos:
- Determinar si ambas variables están correlacionadas, es decir, si para valores más bajos o más altos de una variable, los valores de la otra variable tienden a ser igualmente más bajos o más altos.
- Predecir el valor de una variable, tomando determinado valor de la otra variable.
- Estimar el nivel de correspondencia entre los valores de ambas variables.
¿Qué es el coeficiente de correlación de Pearson?
El Coeficiente de Correlación de Pearson es una medida de la correspondencia o relación lineal entre dos variables cuantitativas aleatorias. En palabras más simples se puede definir como un índice utilizado para medir el grado de relación que tienen dos variables, ambas cuantitativas.
Teniendo dos variables, la correlación facilita que se hagan estimaciones del valor de una de ellas, con conocimiento del valor de la otra variable.
Este coeficiente es una medida que indica la situación relativa de los sucesos respecto a las dos variables, es decir, representa la expresión numérica que indica el grado de correspondencia o relación que existe entre las 2 variables. Estos números varían entre límites de +1 y -1.
¿Cómo se calcula?
Para contar con una guía que permita:
- Establecer la variación contigua de las dos variables
- Comparar los distintos casos entre sí
Para ello se hace uso del coeficiente de correlación de Pearson, definido como la covarianza que se da entre dos variables tipificadas y se calcula con la siguiente expresión:
¿Cómo ese interpreta el coeficiente de correlación de Pearson?
Su dimensión indica el nivel de asociación entre las variables.
- Cuando es menor a cero (r < 0) Se dice que hay correlación negativa: Las variables se correlacionan en un sentido inverso.
A valores altos en una de las variables, le suelen corresponder valores bajos en la otra variable y viceversa. Cuánto el valor esté más próximo a -1 dicho coeficiente de correlación más evidente será la covariación extrema.
Si r= -1 se habla de correlación negativa perfecta, la cual supone una determinación absoluta entre ambas variables, en sentido directo coexiste una relación lineal perfecta de pendiente negativa.
- Cuando es mayor a cero (r > 0) Se dice que hay correlación positiva: Ambas variables se correlacionan en un sentido directo.
A valores altos en una de las variables, le corresponden valores altos en la otra variable e igualmente en una situación inversa sucede con los valores bajos. Cuánto más próximo a +1 se encuentre el coeficiente de correlación más evidente será la covariación.
Si r = 1 Se habla de correlación positiva perfecta, la cual supone una determinación absoluta entre las variables, en sentido directo coexiste una relación lineal perfecta de pendiente positiva).
- Cuando es igual a cero (r = 0) Se dice que las variables están incorrectamente relacionadas, no puede es posible establecer algún sentido de covariación.
No existe relación lineal, pero esto no implica necesariamente que las variables sean independientes, pudiendo existir relaciones no lineales entre las variables.
Cuando las dos variables son independientes se dice que no están correlacionadas, aunque el resultado de reciprocidad no es necesariamente cierto.
Para concluir se puede decir que se ve más difícil de lo que resulta ser, sobre todo si se cuenta con tecnología avanzada, pues hoy día existen múltiples programas que facilitan esta labor de cálculo e interpretación del coeficiente de Pearson.


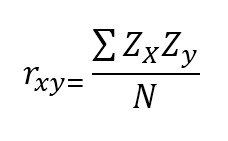
Buenos días. En el penúltimo párrafo hay un error. Tiene que decir: Cuando son independientes se dice están NO CORRELACIONADAS.
Hola Anna, muchas gracias, tienes razón, ya corregí el error.
Saludos
me gustria saber si una correlación baja, por ejemplo 0,33 puede ser significativa y que significa esto.
muchas gracias.